An Infinite Hotel Can Be Fully Booked, Here’s How

Imagine you’re on vacation and your hotel reservation gets canceled. Bummer, you’ll have to find another place to stay, right? You start googling for accommodations when you stumble upon this ad. It mentions a hotel that seemingly has an infinite number of rooms.

They’ll surely have a room available for you, right? You arrive at the hotel, and you’re greeted at the check-in desk by the hotel manager. This receptionist in particular sure does look special. You’ll soon find out why.

He starts by saying all his rooms are booked. The infinite number of rooms are all filled by an infinite number of guests. But wait, the manager might have a solution to still check you in. Told you he was special!

He begins to explain that all the rooms in the hotel are numbered starting from Room Number 1. It goes on to Room Number 2, then 3, moving forward infinitely. At this hotel, there is only one person allowed per room. So, if there is one person in each one of the rooms, how will he make space for you?

Simple: he asks each one of the guests to move down a room. This way, the person staying in Room Number 1 moves over to Room Number 2, that person in Room Number 3, and so on. Once every one of those infinite numbers of guests moves down a room, the first one becomes available for you to stay.

While you are waiting at the reception, a bus shows up, wanting to check in too. 100 guests are waiting outside in the bus. The receptionist applies the same strategy. He moves everyone down 100 rooms until the first 100 rooms become empty and ready to receive guests.

Word rapidly spreads around that there’s a hotel that can fit a lot of guests. Obviously more buses like this one start to arrive. And they’re not just a lot of buses. An infinite number of buses with an infinite number of passengers get lined up at the hotel entrance.

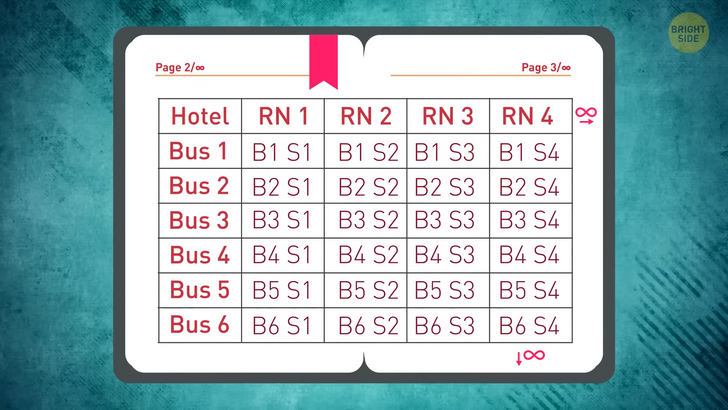
Our receptionist is clever yet again. He opens his infinite agenda, with an infinite number of pages, and starts preparing a table. This one too has an infinite number of columns and rows. In this table, there’s a row for each bus, with the row at the top for all the people that are already in the hotel. He uses the columns to show the position each person occupies.

He’s got Room Number 1, Room Number 2, and so on. He moves on to fill the table with Bus One, Seat 1, then Bus 1, Seat 2. His goal is to make sure each person gets their unique code. This code is made out of a combination of the vehicle and the seat number. He then proceeds to show everyone how he’ll assign the rooms.

Starting with the top left corner of his table, he draws a line that zigzags back and forth across the table, going over each person exactly once. If he could pull at that line from each end, he’d transform an infinite-by-infinite table into one single row. Once the order from that line is defined, he assigns each room number to its designated visitor. Everyone fits once again.

Just as our brilliant receptionist is about to take a break, a big bus appears at the hotel entrance. Not a regular vehicle, but a party bus. It has no seats. But, as you can already imagine by now, this one has an infinite number of passengers too. As they step down from the bus, you listen to their names. They sure are weird!

Soon enough one of the new party visitors starts to explain why they call each other the way they do. Since there’s an infinite number of them in the bus, they’ve all decided to use unique identifiers only using the letters X and Z. To keep with the theme, these names are also infinitely long.

One person might be named X, X, X, X, X, X, X, X, X, X with letters going on indefinitely, while another may be named XZ, XZ, XZ, XZ, XZ, XZ again, with its name going on forever. After thinking about it for a bit, you figure out that there’s a person for each possible infinite sequence of these two letters.

But just as the people from the party bus start entering the hotel, the receptionist says that he’s not able to fit all of them into the hotel. “It might be a bit complicated to explain this time,” he says. “But let me try”. He starts by opening up his infinite agenda once again. He then proceeds to assign rooms to the people on the bus.

Let’s say Room Number 1 is for the person named X, X, X, X, X, X, X, X, X, X, while Room Number 2 is for the person named XZ, XZ, XZ, XZ, XZ, XZ. To finish up, he’d technically have to keep going, allocating a different string of Xs and Zs to each of his infinite number of rooms. “Here’s where it gets tricky” he says “because even if we complete this infinite list of names, I can still name a person who won’t be assigned a room.”

All you have to do to figure out who that person is, is to take the first letter of the first name and switch it, so X becomes Z. Then you take the second letter of the second name and switch it from Z to an X. If you keep doing that, the name you write down is surely not going to appear on the list.

You might have stumbled upon a hotel with an infinite number of rooms, but that’s not to say it can fit literally “everyone”. Because those rooms are infinite, but they are countably infinite. Even if it would take forever, you could technically count all the rooms in the hotel.

The reason why you can’t squeeze all the people from the party bus is that those people are uncountably infinite. There’s no systematic way to identify them. When you look at it this way, it does make you think: are some infinities bigger than others? This theory is called “David Hilbert’s infinite grand hotel, and it’s not the only one of its kind.”

The Friendship theory is a funny one too. It means that most people have fewer friends than their friends have. So if you have three friends, chances are that your friends have more than three friends each. It’s like a puzzle — it’s hard to figure out why this happens, but it’s true!

It was first noticed back in 1991 by a sociologist named Scott Feld. He made this unusual discovery when looking at existing social networks. He calculated the average number of friends that a person has and then compared this number to the average number of friends those respective friends had too. The interesting part happened when he noticed the second number is always bigger.

The problem is, there’s no logical explanation for this phenomenon. Why is this important, you might ask? Because it affects the way we perceive ourselves in relation to others. Most of us look at our friends as being happier, richer, and more popular than they are. But it’s important to remember that almost everyone is in the same situation.

Then there are Zeno’s theories, which are puzzles about motion. They ask questions like “If you have to take half of the steps to get somewhere, and then half of those steps, and then half of those steps... will you ever get there?” The answer is yes! Even though it might seem like you’ll never get to the end, if you keep taking half of the steps, you will eventually get there.

It may seem weird, but all these theories are in fact paradoxes. In math, they are mathematical conclusions so absurd that it is difficult to understand even though every step you took before reaching that said conclusion is correct. In most scenarios, the paradox is the contradiction of the statements themselves. In David Hilbert’s infinite grand hotel, for example, these statements are that the hotel can be fully booked and have rooms available at the same time.